En esta página encontrarás la explicación de los diferentes métodos que existen para determinar la posición relativa de dos rectas en el plano (en R2). Además, verás varios ejemplos y podrás practicar con ejercicios resueltos paso a paso.
Índice
¿Cuál es la posición relativa de dos rectas en el plano?
Antes de ver las posiciones relativas entre dos rectas en el plano, evidentemente debes saber exactamente qué es una recta, lo puedes encontrar en la definición de recta.
Así pues, cuando trabajamos con dos dimensiones (en R2), existen 3 posibles tipos de posiciones relativas entre dos rectas:
Rectas secantes
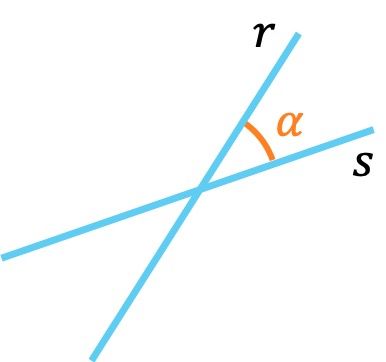
Dos rectas secantes tienen un solo punto en común.
Rectas paralelas
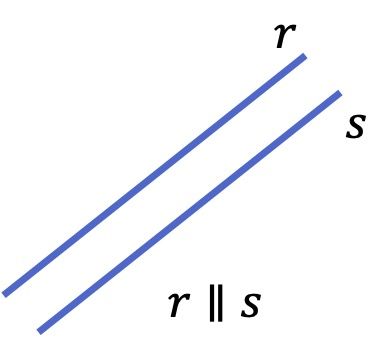
Dos rectas son paralelas si no tienen ningún punto en común. Es decir, si nunca se cruzan.
Rectas coincidentes

Dos rectas son coincidentes si todos sus puntos son comunes.
Por otro lado, el ángulo entre dos rectas en el plano también depende de su posición relativa:
- Las rectas secantes se cortan formando un ángulo entre 0º (no incluido) y 90º (incluido). Además, si justo hacen un ángulo recto de 90º, significa que las dos rectas son perpendiculares.
- Las rectas paralelas forman un ángulo de 0º, ya que tienen la misma dirección.
- Y, por la misma razón, las rectas coincidentes también forman un ángulo de 0º entre sí.
Si quieres saber cómo se calcula el ángulo que forman dos rectas, puedes consultar la fórmula del ángulo entre dos rectas. Aquí encontrarás una explicación detallada de cómo determinar el ángulo que hay entre dos rectas, junto con varios ejemplos e, incluso, ejercicios resueltos para poder practicar y entender bien el concepto.
Cómo hallar la posición relativa de dos rectas en el plano
Saber la posición relativa entre dos rectas en un espacio bidimensional depende de la forma en la que estén expresadas las rectas:
- Vectores directores de las rectas: si dos rectas tienen un vector director diferente, estas deben ser necesariamente secantes. En cambio, si las coordenadas de sus vectores directores son iguales o proporcionales, pueden ser paralelas o coincidentes (se debe comprobar si tienen algún punto en común).
- Ecuación explícita: cuando dos rectas tienen distinta pendiente
son secantes. Por contra, si las rectas tienen la misma pendiente pero diferente ordenada en el origen
son paralelas. Finalmente, dos rectas son coincidentes cuando tienen pendientes y ordenadas en el origen iguales.
- Ecuación general (o implícita): dos rectas con coeficientes A y B no proporcionales siempre serán secantes. Sin embargo, serán paralelas cuando estos dos parámetros sean proporcionales entre sí pero no con el coeficiente C. Y, por último, cuando los tres términos son proporcionales implica que las rectas son coincidentes.
Si tienes alguna duda de las ecuaciones de la recta anteriores, puedes consultar la explicación de las ecuaciones de la recta en el plano. Aquí encontrarás la fórmula de todas las ecuaciones de la recta, cómo se calculan, ejemplos y ejercicios resueltos de las ecuaciones de la recta.
En la siguiente tabla tienes un resumen de las propiedades anteriores:

A continuación vamos a ver dos ejemplos de cómo determinar la posición relativa entre dos rectas:
Ejemplo 1
- Halla la posición relativa entre las siguientes dos rectas definidas en forma de ecuación explícita:
Las dos rectas tienen la misma pendiente:
Pero tienen diferente ordenada en el origen:
Por tanto, como tienen la misma pendiente pero diferente ordenada en el origen, las rectas son paralelas.
Ejemplo 2
- Determina la posición relativa entre las siguientes dos rectas expresadas con su ecuación implícita (o general):
Ambas rectas están expresadas en forma de ecuación explícita, por lo tanto, debemos mirar si alguno de sus coeficientes son proporcionales:
Los 3 términos de las rectas son proporcionales, por lo que las rectas son coincidentes.
Determinar la posición relativa de dos rectas en el plano con un sistema de ecuaciones
Otra manera de averiguar la posición relativa entre dos rectas es analizando el sistema de ecuaciones formado por las ecuaciones de las rectas:
- Si el sistema tiene una única solución, las rectas son secantes. Además, el punto de corte de las dos rectas es la solución del sistema.
- Si se trata de un sistema sin solución, indica que las rectas no tienen ningún punto en común y, en consecuencia, son rectas paralelas.
- Si el sistema tiene infinitas soluciones, significa que las rectas tienen todos los puntos en común y, por tanto, son rectas secantes.
Ejemplo 3
- Calcula la posición relativa de las siguientes dos rectas mediante un sistema de ecuaciones:
Para hallar la posición relativa de las dos rectas, debemos resolver el siguiente sistema de ecuaciones lineales formado por ambas rectas:
En este caso, solucionaremos el sistema con el método de sustitución. Así que despejaremos la variable de la segunda ecuación y la sustituiremos en la primera ecuación:
Y una vez sabemos cuánto vale la incógnita sustituimos su valor en la expresión de hallada de
De modo que hemos obtenido 1 sola solución del sistema de ecuaciones compuesto por las dos rectas, por lo que las dos rectas son secantes. Y el punto donde se cortan es la solución del sistema, es decir, el punto
Ejercicios resueltos de posición relativa de dos rectas en el plano
Ejercicio 1
Determina si las siguientes rectas son secantes, paralelas o coincidentes:
Las dos rectas están expresadas en forma de ecuación implícita (o general), por tanto, debemos ver si alguno de sus coeficientes son proporcionales:
Solamente los coeficientes A y B de las rectas son proporcionales entre sí, y no con el coeficiente C. De modo que las dos rectas son paralelas.
Ejercicio 2
Encuentra la posición relativa entre las siguientes dos rectas expresadas en forma de ecuaciones paramétricas:
Podríamos resolver el sistema de ecuaciones formado por las dos rectas para hallar su posición relativa. Sin embargo, como están en forma de ecuaciones paramétricas, podemos encontrar sus vectores directores fácilmente y si no son proporcionales significará que las rectas son secantes. Y en tal caso no gastaremos tanto tiempo resolviendo todo un sistema de ecuaciones.
De manera que las coordenadas cartesianas del vector director de cada recta son los números de delante del parámetro
Una vez sabemos los vectores directores, comprobamos su proporcionalidad:
Los vectores directores no son proporcionales, por tanto, las rectas son secantes.
Ejercicio 3
Indica si las siguientes rectas son secantes, paralelas o coincidentes y encuentra también algún punto de intersección entre ellas (si tiene).
Las dos rectas están definidas por su ecuación explícita y tienen diferente pendiente:
Al tener distinta pendiente, las rectas son secantes.
Por tanto, como las rectas son secantes, tendrán 1 punto en común y para calcularlo debemos resolver el sistema de ecuaciones formado por las dos rectas:
En este caso, resolveremos el sistema con el método de igualación porque las dos ya están despejadas:
Y una vez tenemos la incógnita sustituimos su valor en cualquier expresión de
para determinar cuánto vale:
Así que el punto de intersección de las dos rectas es el resultado del sistema:
Ejercicio 4
Calcula el valor de las incógnitas y
para que las siguientes dos rectas sean paralelas:
Las rectas están descritas en forma de ecuación general (o implícita). Por tanto, para que las dos rectas sean paralelas, sus coeficientes A y B deben ser proporcionales, o dicho de otra forma, se debe cumplir la siguiente ecuación:
Así que debemos resolver la ecuación anterior para obtener el valor de la incógnita Para ello, multiplicamos las fracciones en cruz:
Por otro lado, para que las rectas sean paralelas sus términos independientes no pueden ser proporcionales con los otros coeficientes:
Por tanto, al igual que antes, resolvemos la inecuación multiplicando las fracciones en cruz:
En definitiva, para que las dos rectas sean paralelas debe ser 2 y
puede ser cualquier número real menos 3.
Ejercicio 5
Encuentra la ecuación explícita de la recta paralela a la recta y que pasa por el punto
Siendo la recta
Para que la recta sea paralela a la recta ambas deben tener la misma pendiente. Y la pendiente de la recta
es 2:
Por tanto, la ecuación de la recta que debemos hallar será de la siguiente forma:
Y una vez sabemos la pendiente de la recta, podemos calcular la ordenada en el origen sustituyendo el punto que pertenece a la recta en la ecuación de la recta:
Por lo que la ecuación explícita de la recta es:
Si has llegado hasta aquí quiere decir que ya dominas las posiciones relativas entre dos rectas en el plano. ¡Buen trabajo!
Pero una cosa que muchos se preguntan es… ¿y realmente para qué sirve saber la posición relativa entre dos rectas?
Pues una de las aplicaciones de la posición relativa entre rectas es poder averiguar la distancia que hay entre 2 rectas, ya que el cálculo de la distancia entre dos rectas depende de su posición relativa:
- Si las rectas son secantes o coincidentes la distancia es nula.
- En cambio, cuando las rectas son paralelas se debe aplicar una fórmula concreta. Si estás más interesad@, puedes consultar cómo se calcula la distancia entre dos rectas paralelas.


Muchas gracias por crear páginas como estas, me ayudan mucho
¡Un placer Agustin!
Terriblemente gracias! Me salvaron el final ;´)
¡Me alegro que te haya ido bien! ¡Seguro que apruebas el examen! 😉
Muy buena explicación……..me ayudaron mucho, una pregunta no tienen canal de YouTube para poder ver vídeos explicativos 📱
¡Muchas gracias Lizeth! 🙂
No, de momento no tenemos canal de YouTube, aunque es una opción que contemplamos para el futuro.
¡Pero tenemos otras páginas webs especializadas en otros temas de matemáticas! ¡Te las dejo a continuación para que puedas echarles un vistazo! 😉
Hola muy buena explicación, pero que en que bibliografías se basa? Me gustaría conocer eso porque se acerca una prueba
Hola Eugenio, todos los artículos de la página web están basados en el conocimiento de su autor. Cualquier otra duda que tengas puedes preguntar que intentaré responderte.