▷ Planos Paralelos: ejemplos, propiedades, ejercicios resueltos,...

En esta página encontrarás todo sobre los planos paralelos: cuándo dos planos son paralelos, las ecuaciones de dos planos paralelos, ejemplos, ejercicios resueltos, propiedades,…

Índice

¿Qué son dos planos paralelos?

En geometría analítica, dos planos son paralelos cuando siempre mantienen una misma distancia entre sí. Por lo tanto, dos planos paralelos nunca se cortan y no tienen ningún punto en común.

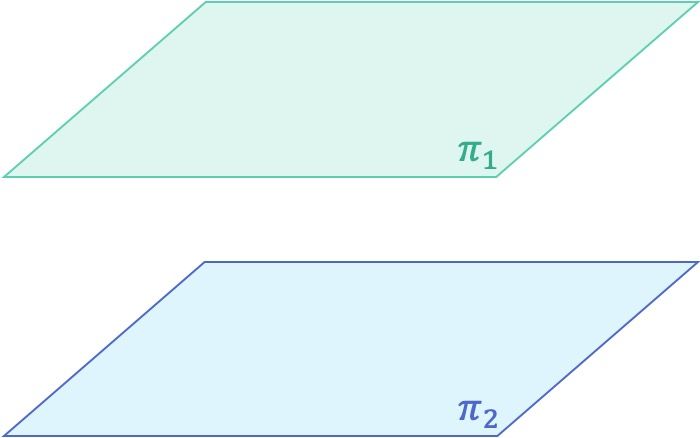
Dos planos posicionados paralelamente no es la única posición relativa posible entre los planos, ya que dos planos en el espacio (en R3) también pueden ser secantes o coincidentes.

¿Cómo saber si dos planos son paralelos?

Una vez vista la definición de los planos paralelos, veamos cómo se puede determinar si dos planos son paralelos o no.

Partiendo de la ecuación general (o implícita) de dos planos distintos:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

Los 2 planos serán paralelos si sus coeficientes A, B y C son proporcionales entre sí y no con el coeficiente D. Es decir, el paralelismo entre dos planos tiene lugar cuando se cumple la siguiente ecuación:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Ejemplo de dos planos paralelos

Por ejemplo, los siguientes dos planos son paralelos:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

Los planos son paralelos porque los coeficientes de las variables X, Y, Z son proporcionales entre ellos, pero no con los términos independientes:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Calcular la distancia entre dos planos paralelos

Dos planos paralelos siempre están a la misma distancia, por lo tanto, para encontrar la distancia entre dos planos paralelos podemos coger un punto de cualquiera de los dos planos y calcular la distancia que hay desde ese punto hasta el otro plano. Por lo tanto, para calcular la distancia entre 2 planos paralelos es necesario saber la fórmula de la distancia de un punto a un plano.

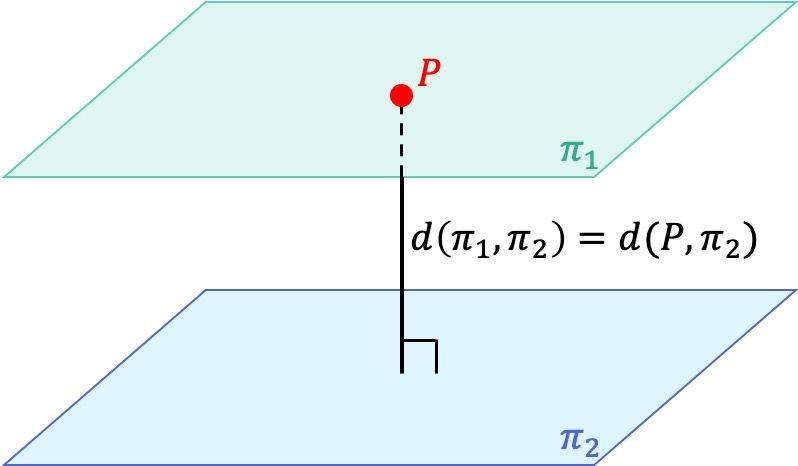
Este es un método para hallar la distancia entre dos planos paralelos. Sin embargo, existe otra manera aún más fácil para hacerlo cuando los coeficientes A, B y C de las ecuaciones de los dos planos coinciden:

Sean la ecuaciones generales (o implícitas) de dos planos paralelos:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La fórmula para calcular la distancia entre dos planos paralelos es:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

De modo que seguramente es más fácil averiguar la distancia entre dos planos paralelos mediante la fórmula ya que solamente consiste en aplicar la fórmula y ya esta, pero esto depende del problema. Además, creemos que es mejor explicar las dos formas que hay de calcular la distancia para que tú puedas escoger cuál prefieres.

Ejemplo del cálculo de la distancia entre dos planos paralelos

A modo de ejemplo, vamos a calcular la distancia entre los siguientes dos planos:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

En primer lugar, debemos comprobar que se trata de dos planos paralelos. Así pues, todos los coeficientes de las ecuaciones de los planos son proporcionales excepto los términos independientes, por lo que efectivamente son dos planos paralelos.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

En este caso los términos A, B y C de las ecuaciones de los dos planos no coinciden, pero podemos lograrlo dividiendo toda la ecuación del segundo plano entre dos:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

De manera que las ecuaciones de los dos planos ahora ya tienen los mismos coeficientes A, B y C. Por tanto, podemos calcular fácilmente la distancia entre ambos planos con la fórmula de la distancia entre dos planos paralelos:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Sustituimos los valores y resolvemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

De forma que la distancia entre un plano y el otro plano es igual a la unidad.

Propiedades de los planos paralelos

Las características de los planos paralelos son las siguientes:

Propiedad reflexiva: todo plano es paralelo a sí mismo.

$\pi_1 \parallel \pi_1$

Propiedad simétrica: si un plano es paralelo a otro, aquel plano también es paralelo al primero. Esta propiedad también la poseen los planos perpendiculares.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Propiedad transitiva: si un plano es paralelo a otro plano, y este segundo plano es a la vez paralelo a un tercer plano, el primer plano también es paralelo al tercer plano.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$

2 comentarios en “Planos paralelos”

brian
30/09/2021 a las 15:47

está mal, D2 es 2 no 1!.

Responder
1. Geometría Analítica
  02/10/2021 a las 13:42
  
  Hola Brian,
  
  Es cierto que en la ecuación original del plano el término independiente es un 2, sin embargo, esa ecuación hay que dividirla entre dos para que las ecuaciones de los dos planos tengan los mismos coeficientes A, B y C y así poder aplicar la fórmula. Por lo tanto, el 1 está bien.