▷ Hallar la distancia de un punto a un plano (fórmula y ejemplos)

En esta página encontrarás cómo se calcula la distancia entre un punto y un plano en el espacio (fórmula). Además, podrás ver ejemplos y practicar con ejercicios resueltos paso a paso.

Índice

¿Cuál es la distancia de un punto a un plano?

En geometría analítica, la distancia de un punto a un plano es la distancia más corta que existe entre el punto y cualquier otro punto del plano. Esta distancia corresponde a longitud del segmento perpendicular al plano que va desde el punto hasta el plano.

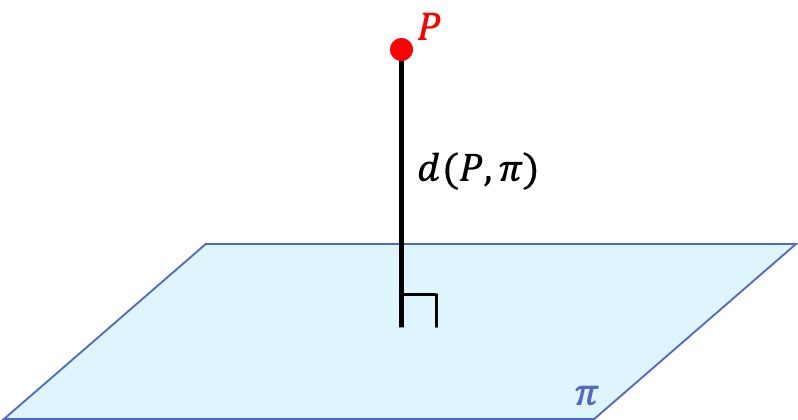
qué es la distancia de un punto a un plano

Fórmula de la distancia de un punto a un plano

Una vez hemos visto exactamente el concepto de la distancia entre un punto y un plano, veamos ahora la fórmula para calcular dicha distancia:

Dados un punto y la ecuación general (o implícita) de un plano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

La fórmula de la distancia de un punto a un plano es:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

La demostración de la fórmula de la distancia de un punto a un plano es bastante tediosa y larga, por lo que no la haremos en esta página.

Por otro lado, si al aplicar la fórmula obtenemos un resultado igual a cero, evidentemente significa que la distancia entre el punto y el plano es nula y, por tanto, el punto forma parte de ese plano.

Finalmente, fíjate que para poder aplicar la fórmula el plano debe estar definido en forma de ecuación general (o implícita). De modo que si estuviera expresado mediante otro tipo de ecuación del plano, primero tendríamos que transformarlo en ecuación general y luego emplear la fórmula.

Ejemplo de cómo calcular la distancia de un punto a un plano

Para que puedas ver cómo se determina numéricamente la distancia entre un punto y un plano, a continuación vamos a resolver un ejemplo:

Calcula la distancia entre el punto P y el plano π. Siendo dichos punto y plano:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Para hallar la distancia que hay desde el punto hasta el plano, simplemente tenemos que aplicar la fórmula vista en el apartado de arriba:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Ahora sustituimos el valor de cada incógnita en la fórmula:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

Y, finalmente, hacemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Fíjate que en el numerador de la fracción hay un valor absoluto y en el denominador tenemos una raíz cuadrada, de modo que el resultado siempre nos debe dar positivo. Esto es lógico porque las distancias no pueden ser negativas, sino que siempre son positivas.

Calcular la distancia entre dos planos paralelos

Dos planos paralelos siempre están a la misma distancia, por lo tanto, para encontrar la distancia entre dos planos paralelos podemos coger un punto de cualquiera de los dos planos y calcular la distancia que hay desde ese punto hasta el otro plano.

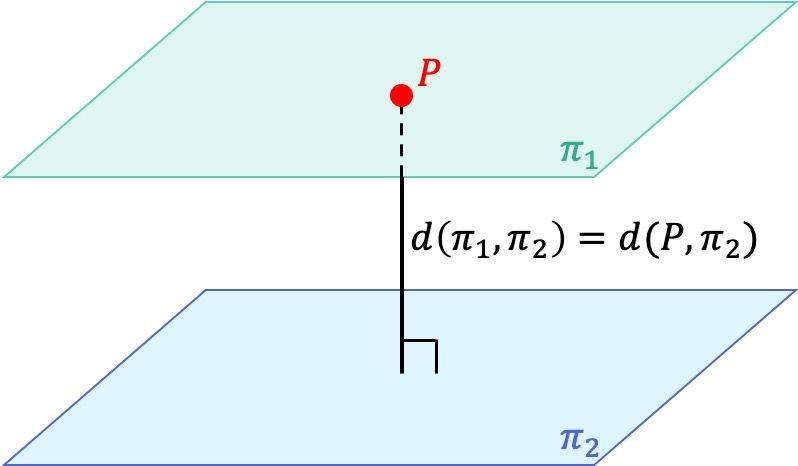
Este es un método para hallar la distancia entre dos planos paralelos. Sin embargo, existe otra manera aún más fácil para hacerlo cuando los coeficientes A, B y C de las ecuaciones de los dos planos coinciden:

Sean las ecuaciones generales (o implícitas) de dos planos paralelos:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La fórmula para calcular la distancia entre dos planos paralelos es:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

De modo que seguramente es más fácil averiguar la distancia entre dos planos paralelos mediante la fórmula ya que solamente consiste en aplicar la fórmula y ya esta, pero esto depende del problema. Además, creemos que es mejor explicar las dos formas que hay de calcular la distancia para que tú puedas escoger cuál prefieres.

Ejemplo del cálculo de la distancia entre dos planos paralelos

A modo de ejemplo, vamos a calcular la distancia entre los siguientes dos planos:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

En primer lugar, debemos comprobar que se trata de dos planos paralelos. Así pues, todos los coeficientes de las ecuaciones de los planos son proporcionales excepto los términos independientes, por lo que efectivamente son dos planos paralelos.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

En este caso los términos A, B y C de las ecuaciones de los dos planos no coinciden, pero podemos lograrlo dividiendo toda la ecuación del segundo plano entre dos:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

De manera que las ecuaciones de los dos planos ahora ya tienen los mismos coeficientes A, B y C. Por tanto, podemos calcular fácilmente la distancia entre ambos planos con la fórmula de la distancia entre dos planos paralelos:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Sustituimos los valores y resolvemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

De forma que la distancia entre un plano y el otro plano es igual a la unidad.

Ejercicios resueltos de distancia de un punto a un plano

Ejercicio 1

Calcula la distancia entre el punto P y el plano cuya ecuación cartesiana (o general) es:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

Ver solución

Para calcular la distancia que hay desde el punto hasta el plano, debemos utilizar la fórmula correspondiente:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sustituimos el valor de cada parámetro en la fórmula:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

Y, por último, hacemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Ejercicio 2

Halla la distancia entre el punto P y el plano π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

Ver solución

Antes de usar la fórmula de la distancia de un punto a un plano, primero debemos expresar el plano en forma de ecuación implícita (o general):

$\pi: \ -5x+y+2z=0$

Y ahora ya podemos usar la fórmula para determinar la distancia que hay del punto al plano:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sustituimos el valor de cada término en la fórmula:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

Y, para terminar, hacemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Ejercicio 3

Utiliza la fórmula de la distancia entre un punto y un plano para determinar si el punto P pertenece al plano π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

Ver solución

Para verificar si el punto pertenece al plano podemos calcular la distancia entre ambos: si la distancia es nula implica que el punto sí que es del plano, en cambio, si la distancia es diferente de 0 significa que el punto está fuera del plano.

Por tanto, determinamos la distancia entre el punto y el plano a partir de la fórmula:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

La distancia entre el punto y el plano es equivalente a cero, con lo que efectivamente el punto pertenece al plano.

Ejercicio 4

Encuentra la distancia entre los siguientes dos planos:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

Ver solución

Primero de todo, debemos comprobar que se trata de dos planos paralelos. Todos los coeficientes de las ecuaciones de los dos planos son proporcionales excepto los términos independientes, por lo que efectivamente se trata de dos planos paralelos.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

En este caso calcularemos la distancia entre los dos planos con la fórmula, ya que sus coeficientes A, B y C son iguales:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Entonces, sustituimos los valores en la fórmula y hacemos las operaciones:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Ejercicio 5

Averigua la distancia entre los siguientes dos planos paralelos:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

Ver solución

El primer plano está definido en forma de ecuaciones paramétricas, por lo que para aplicar la fórmula de la distancia entre dos planos paralelos primero deberíamos pasarlo a forma de ecuación general y esto conlleva muchos cálculos y tiempo. Por tanto, es más rápido si cogemos un punto de ese plano y calculamos la distancia de dicho punto hasta el otro plano.

Así pues, las coordenadas de un punto por el que pasa el plano π₁ corresponden a los términos independientes de cada ecuación paramétrica:

$P(3,-2,5)$