Lugar geométrico (definición y ejemplos)

En esta página encontrarás la explicación de qué es un lugar geométrico. Además, podrás ver varios ejemplos de lugares geométricos para entender del todo el concepto.

¿Qué es un lugar geométrico?

En geometría analítica, un lugar geométrico es un conjunto de puntos que cumplen con una determinada condición geométrica.

Puede que con solo la definición de lugar geométrico no te haya quedado muy claro el concepto, porque es difícil de entender. Así que veamos un ejemplo para completar su significado:

Seguro que sabes qué son las circunferencias, pues bien, una circunferencia es un ejemplo claro de un lugar geométrico ya que todos los puntos del plano que forman un circunferencia cumplen una misma propiedad geométrica: todos los puntos de una circunferencia están a la misma distancia de otro punto fijo (el centro de dicha circunferencia).

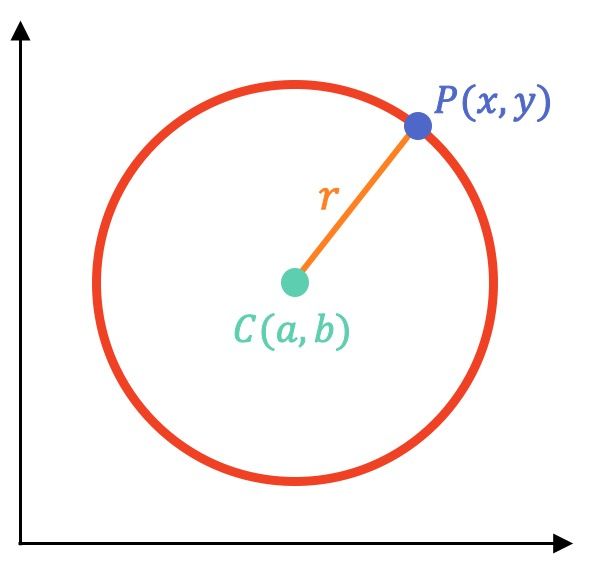
Por otro lado, esta propiedad geométrica que deben satisfacer todos los puntos de un lugar geométrico se debe poder expresar matemáticamente mediante ecuaciones algebraicas.

Así pues, los lugares geométricos sirven para definir diferentes figuras geométricas, a continuación tienes los ejemplos de lugares geométricos más importantes.

Ejemplos de lugares geométricos

Una vez hemos visto qué significa el lugar geométrico de los puntos, pasamos ahora a ver varios ejemplos de lugares geométricos. Entre ellos destacan las denominadas secciones cónicas, que son la circunferencia, la elipse, la parábola y la hipérbola.

Este grupo geométrico se llama secciones cónicas debido a que todas ellas se pueden obtener a partir de un cono. Si quieres saber cómo se hace puedes consultar nuestra página de las secciones cónicas, donde encontrarás una explicación detallada de qué son y de por qué son tan importantes.

Circunferencia

Como hemos visto antes, cualquier circunferencia se trata de un lugar geométrico que, en particular, verifica la siguiente condición:

La circunferencia es el lugar geométrico de los puntos del plano cartesiano que equidistan de un punto fijo llamado centro.

Como bien sabes, esa distancia entre el centro de la circunferencia y uno de sus puntos se llama radio.

La circunferencia es una figura geométrica de especial relevancia para las matemáticas, ya que tiene muchas aplicaciones. Puedes consultar cómo definir numéricamente una circunferencia mediante la ecuación de la circunferencia. Además, aquí hallarás todos los tipos de ecuaciones de la circunferencia, así como problemas y ejercicios resueltos relacionados para poder practicar.

Elipse

La elipse es una línea curva, cerrada y plana muy parecida a la circunferencia, pero su forma es más ovalada.

En concreto, la elipse es el lugar geométrico de todos los puntos del plano XY cuya suma de distancias a otros dos puntos fijos (llamados focos F y F’) es constante.

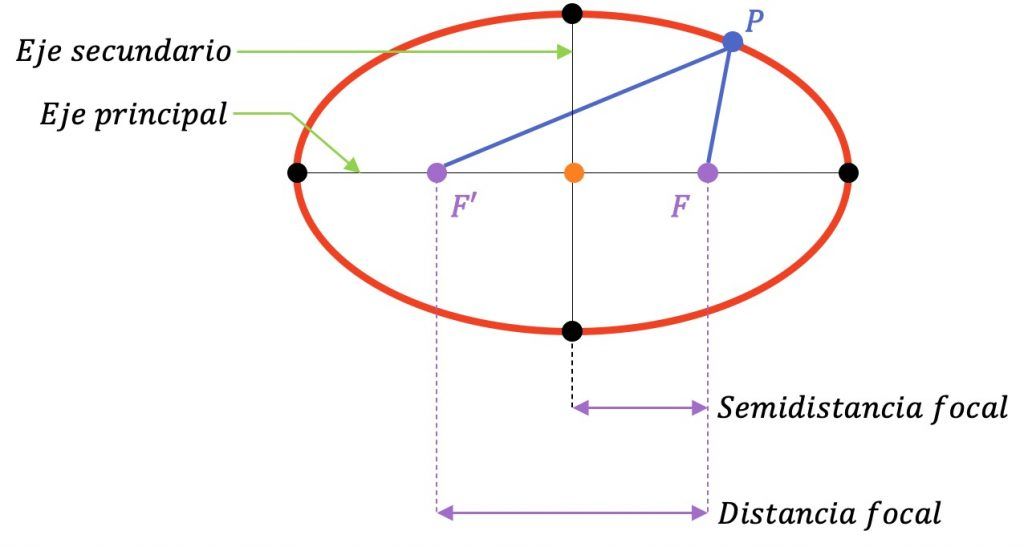
La forma de expresar analíticamente una elipse es muy parecida a la de una circunferencia. Si quieres, puedes ir a este enlace para saber cómo es la ecuación reducida de la elipse, aquí también hallarás cuáles son los elementos que definen una elipse e incluso distintos ejemplos y ejercicios resueltos.

Parábola

En matemáticas, una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (llamado foco) y de una recta fija (denominada directriz).

A continuación tienes representada gráficamente una parábola (curva de color naranja).

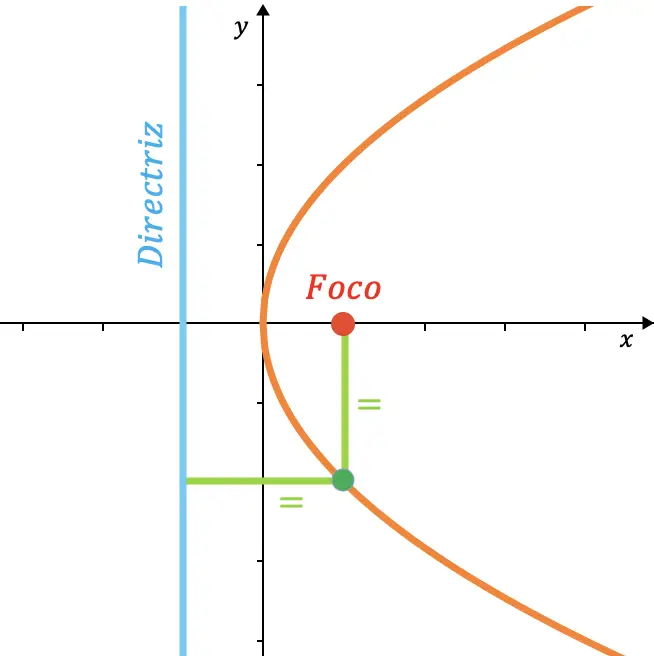
Nos hemos esforzado en concentrar todo lo que debes saber sobre la parábola en una sola página. Allí se explican todos los elementos que describen una parábola, sus diferentes ecuaciones, las propiedades que tiene, sus aplicaciones reales,… En definitiva, en el siguiente enlace podrás saber todo lo necesario sobre la parábola (matemáticas).

Hipérbola

Una hipérbola es el lugar geométrico de los puntos del plano que cumplen la siguiente condición: el valor absoluto de la diferencia de las distancias desde un punto cualquiera de la hipérbola hasta dos puntos fijos (llamados focos) debe ser constante.

Además, el valor de la resta de esas dos distancias siempre es equivalente a la distancia entre los dos vértices de la hipérbola.

En la siguiente representación gráfica puedes ver que una hipérbola siempre está formada por dos ramas:

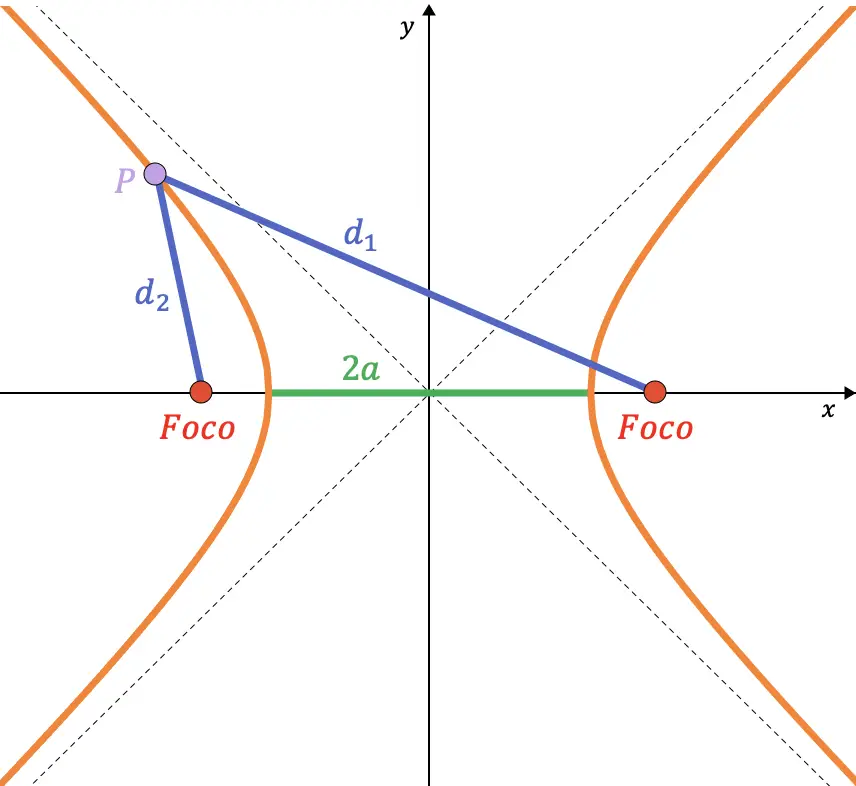
Como puedes intuir, el valor del parámetro de una hipérbola es fundamental para las hipérbolas. En nuestra explicación de la hipérbola, podrás ver por qué es un coeficiente tan importante así como cuáles son todos los elementos que caracterizan una hipérbola. Además, encontrarás cómo es la ecuación de una hipérbola, los distintos tipos de hipérbolas que existen e, incluso, problemas y ejercicios resueltos paso a paso de hipérbolas.

Más ejemplos de lugares geométricos

Los tipos de lugares geométricos que más se analizan en secundaria y bachillerato son los 4 anteriores que hemos visto, pero también hay otros ejemplos de lugares geométricos muy conocidos:

• Mediatriz: la mediatriz es el lugar geométrico de los puntos que equidistan de dos puntos fijos. Además, si esos dos puntos son los extremos de un segmento, la mediatriz es a la vez la recta perpendicular que interseca dicho segmento por su punto medio. Si estás más interesad@, aquí puedes ver cómo se calcula el punto medio de un segmento.
• Bisectriz: la bisectriz es el lugar geométrico de los puntos que equidistan de los lados de un ángulo. Es decir, la bisectriz es la recta que corta un ángulo por la mitad.
• Recta paralela: una recta paralela es el lugar geométrico de los puntos que están a una misma distancia de una determinada recta. O dicho con otras palabras, la distancia entre dos rectas paralelas es siempre igual.