Calcular la excentricidad de la elipse

En esta página encontrarás el significado de la excentricidad de la elipse y cómo se calcula (fórmula). Además, podrás ver ejemplos de cálculos de excentricidades de elipses.

¿Qué es la excentricidad de la elipse?

La excentricidad de la elipse es un parámetro que mide cuánto de redonda o aplanada es una elipse, es decir, la excentricidad de una elipse dice cuánto se parece dicha elipse a una circunferencia.

Por otro lado, recordemos también en qué consiste una elipse: la elipse es el lugar geométrico de todos los puntos de un plano cuya suma de distancias a otros dos puntos fijos (llamados focos F y F’) es constante.

Fórmula de la excentricidad de la elipse

Una vez vista la definición de la excentricidad de la elipse, veamos cómo se calcula a partir de su fórmula:

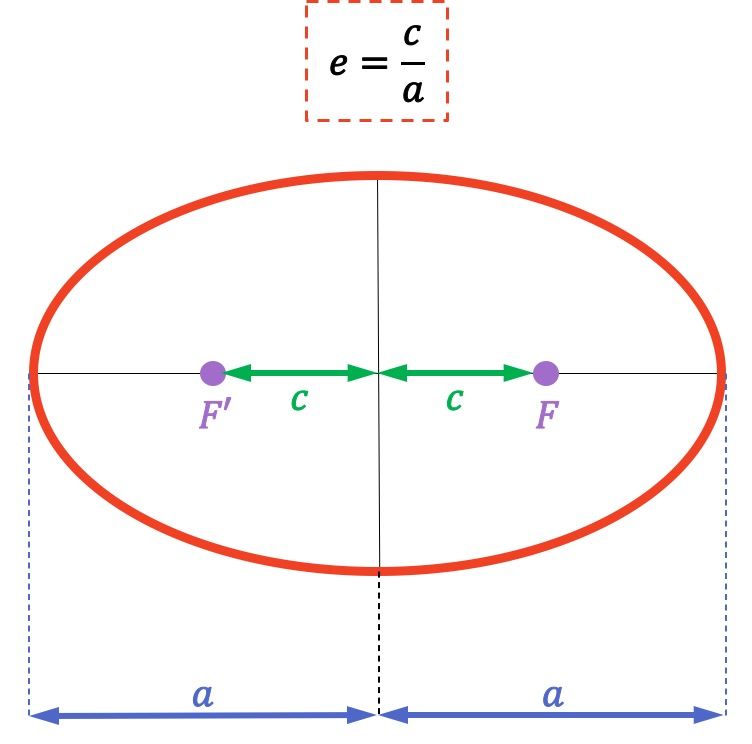
Recordemos que los focos de una elipse son aquellos puntos fijos cuya suma de distancias a cualquier punto de la elipse es constante. Además, la distancia entre los dos focos se llama distancia focal.

El valor de la excentricidad va desde cero, que significa que es una circunferencia perfecta, hasta uno, que implica que se trata de una línea recta horizontal. Evidentemente, tanto el 0 como el 1 no se incluyen porque los objetos geométricos resultantes ya no son elipses.

Por lo tanto, como puedes ver en la representación gráfica de abajo, cuanto más pequeño es el valor de la excentricidad de la elipse más se parece a una circunferencia, en cambio, cuanto más grande es el coeficiente más aplanada es la elipse.

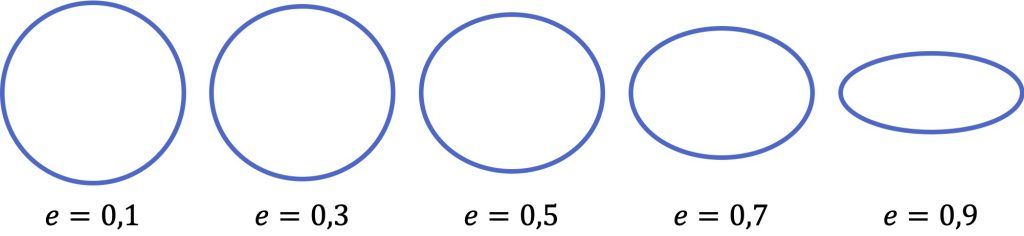
En definitiva, la excentricidad de una elipse es un coeficiente cuyo valor determina la forma que tiene.

Si estás más interesado sobre las características de una elipse, puedes consultar la ecuación de la elipse. En esta página encontrarás una explicación detallada de qué es una elipse, todos sus elementos y cómo se calcula su ecuación. Y, además, podrás ver varios ejemplos, ejercicios y problemas resueltos sobre elipses.

Relación importante para hallar la excentricidad de la elipse

Los distintos elementos de una elipse están relacionados entre sí. Además, las relaciones que hay entre ellos son muy importantes para los ejercicios de elipses, ya que se suelen necesitar para resolver los problemas de elipses y determinar sus ecuaciones.

Como hemos visto más arriba en la explicación del concepto de excentricidad de la elipse, la distancia de cualquier punto de la elipse al foco F más la distancia del mismo punto al foco F’ es constante. Pues ese valor constante es igual al doble de lo que mide el semieje mayor. O dicho de otra forma, la siguiente igualdad se cumple para cualquier punto de una elipse:

Donde y es la distancia del punto P al foco F y F’ respectivamente y es la longitud del semieje focal.

En consecuencia, como el vértice del eje secundario está justo en la mitad del eje principal, la distancia desde este hasta uno de los focos es equivalente a la longitud del semieje principal ():

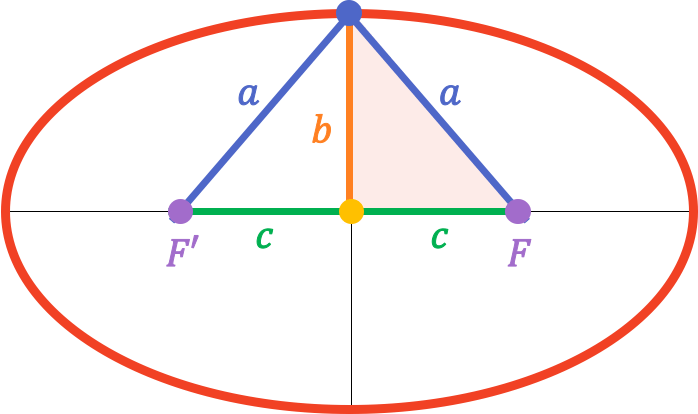
Por tanto, a partir del teorema de Pitágoras, se puede encontrar la relación que existe entre el semieje principal, el semieje secundario y la semidistancia focal de una elipse:

Recuerda también esta otra fórmula porque te será muy útil para calcular el resultado de los ejercicios con elipses.

Ejemplo de cómo calcular la excentricidad de la elipse

A continuación tienes un ejercicio resuelto para ver cómo se calcula la excentricidad de una elipse:

• Halla la excentricidad de la elipse cuyos semieje principal y semieje secundario miden 5 y 3 unidades respectivamente.

Para hallar cuánto vale la excentricidad de la elipse, necesitamos saber la longitud del semieje principal y la longitud del segmento entre un foco y el centro de la elipse. La primera ya la conocemos, por lo que solo nos queda determinar la semidistancia focal.

A partir de la fórmula de la relación entre los elementos de una elipse, podemos calcular cuánto vale la semidistancia focal:

Y cuando ya conocemos el valor de los términos y ya podemos determinar la excentricidad de la elipse: