Ecuaciones paramétricas del plano

En esta página encontrarás cuáles son las ecuaciones paramétricas de un plano y cómo se calculan (fórmula). Además, podrás ver ejemplos y practicar con ejercicios resueltos paso a paso.

¿Qué son las ecuaciones paramétricas de un plano?

En geometría analítica, las ecuaciones paramétricas de un plano son unas ecuaciones que permiten expresar matemáticamente cualquier plano. Para hallar las ecuaciones paramétricas de un plano solo se necesita un punto y dos vectores linealmente independientes que pertenezcan a ese plano.

Fórmula de las ecuaciones paramétricas del plano

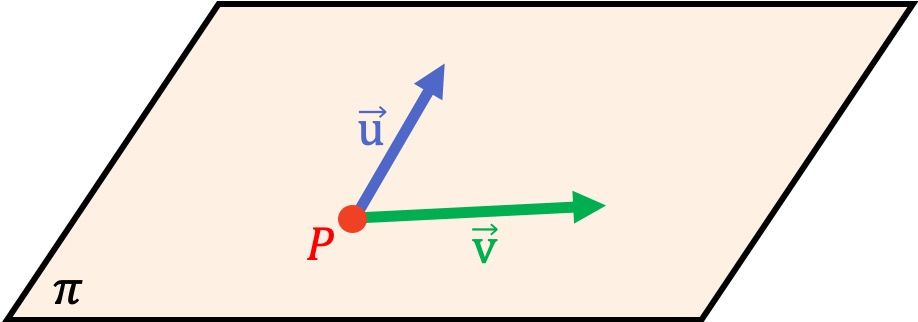
Dados un punto y dos vectores directores de un plano:

\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}

La fórmula de las ecuaciones paramétricas de un plano es:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

Donde \lambda y \mu son dos escalares, es decir, dos números reales.

Es importante que los dos vectores directores de la ecuación del plano sean linealmente independientes, es decir, que tengan una dirección diferente (no paralelos). De lo contrario, la ecuación anterior no representaría ningún plano.

ecuacion parametrica del plano

Por otro lado, ten en cuenta que a parte de la ecuación paramétrica existen otras formas de expresar analíticamente un plano en el espacio (en R3), como por ejemplo la ecuación general del plano. En este enlace encontrarás su fórmula, cómo se calcula a partir de las ecuaciones paramétricas del plano, ejemplos y ejercicios resueltos.

Ejemplo de cómo hallar las ecuaciones paramétricas de un plano

Una vez vista cuál es la ecuación paramétrica del plano, veamos cómo se calcula mediante un ejemplo:

  • Halla las ecuaciones paramétricas del plano que pasa por el punto P(1,3,2) y contiene los vectores \vv{\text{u}}=(2,0,-1) y \vv{\text{v}}=(4,2,3)

Para determinar las ecuaciones paramétricas del plano, simplemente debemos aplicar su fórmula:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

Y ahora sustituimos el punto y cada vector director en la ecuación:

\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}

\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}

Cómo pasar de la ecuación vectorial de un plano a ecuaciones paramétricas

Otro método de determinar las ecuaciones paramétricas de un plano es a partir de la ecuación vectorial de un plano. A continuación puedes ver la demostración.

Sea la ecuación vectorial de un plano cualquiera:

(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)

Primero operamos y realizamos los productos de vectores por los escalares:

(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)

Luego sumamos las componentes:

(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)

Y, finalmente, conseguimos la ecuación paramétrica del plano igualando las coordenadas correspondientes a cada variable por separado:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

Como puedes ver en los dos ejemplos anteriores, encontrar las ecuaciones paramétricas de un plano es relativamente fácil. Sin embargo, se puede complicar un poco en los problemas, por eso más abajo dispones de varios ejercicios resueltos de diferente dificultad para que puedas practicar.

Ejercicios resueltos de ecuaciones paramétricas del plano

Ejercicio 1

Determina las ecuaciones paramétricas del plano que contiene el vector \vv{\text{u}}=(2,1,5) y pasa por los siguientes dos puntos: A(3,2,-1) y B(-2,-1,1).

Para averiguar la ecuación de un plano se necesita un punto y dos vectores y en este caso solo tenemos un único vector, por lo que debemos hallar otro vector director del plano. Para ello, podemos calcular el vector que definen los dos puntos del plano:

\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)

Ahora ya sabemos dos vectores directores del plano y un punto, de modo que utilizamos la fórmula de las ecuaciones paramétricas del plano:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

Y sustituimos los dos vectores y cualquiera de los dos puntos del plano en la ecuación:

\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}

\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}

 

Ejercicio 2

Encuentra las ecuaciones paramétricas del plano que contiene los siguientes tres puntos:

A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)

Para encontrar las ecuaciones paramétricas del plano, necesitamos hallar dos vectores linealmente independientes que pertenezcan al plano. Y, para ello, podemos calcular dos vectores que quedan definidos por los 3 puntos:

\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)

\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)

Las coordenadas de los dos vectores hallados no son proporcionales, por lo que son linealmente independientes entre sí.

Ahora ya conocemos dos vectores directores y un punto del plano, de manera que aplicamos la fórmula de la ecuación paramétrica del plano:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

Y sustituimos los dos vectores y cualquiera de los tres puntos del plano en la ecuación:

\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}

\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}

 

Ejercicio 3

Calcula las ecuaciones paramétricas del plano que queda definido por la siguiente ecuación vectorial:

(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)

Para transformar la ecuación vectorial del plano en ecuación paramétrica, tenemos que operar con las coordenadas y luego despejar cada variable por separado:

(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)

(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)

(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)

\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}

 

Ejercicio 4

Halla las ecuaciones paramétricas del plano que contiene la recta r y es paralelo a la recta s. Siendo las rectas:

\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}

Para hallar las ecuaciones paramétricas del plano necesitamos conocer dos vectores directores y un punto de dicho plano. El enunciado nos dice que contiene la recta r, por tanto, podemos coger el vector director y un punto de esa recta para definir el plano. Además, el enunciado nos dice que el plano es paralelo a la recta s, por lo que también podemos utilizar el vector director de esa recta para la ecuación del plano.

La recta r está expresada en forma de ecuaciones paramétricas, así que las componentes de su vector director son los coeficientes de los términos con el parámetro t:

\vv{r} =(1,-3,2)

Y las coordenadas cartesianas de un punto de esa misma recta son los términos independientes de las ecuaciones paramétricas:

P(1,2,4)

Por otra parte, la recta s está en forma de ecuación continua, de manera que las componentes de su vector director son los denominadores de las fracciones:

\vv{s} =(2,2,-3)

Por tanto, las ecuaciones paramétricas del plano son:

\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}

\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}

\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio