▷ Cómo calcular el ángulo entre una recta y un plano (fórmula y ejemplos)

Aquí encontrarás cómo se calcula el ángulo entre una recta y un plano. También podrás ver ejemplos y, además, practicar con ejercicios resueltos paso a paso de ángulos entre rectas y planos.

Índice

¿Cuál es el ángulo entre una recta y un plano?

El ángulo entre una recta y un plano es el ángulo que forman la recta con su proyección ortogonal en el plano.

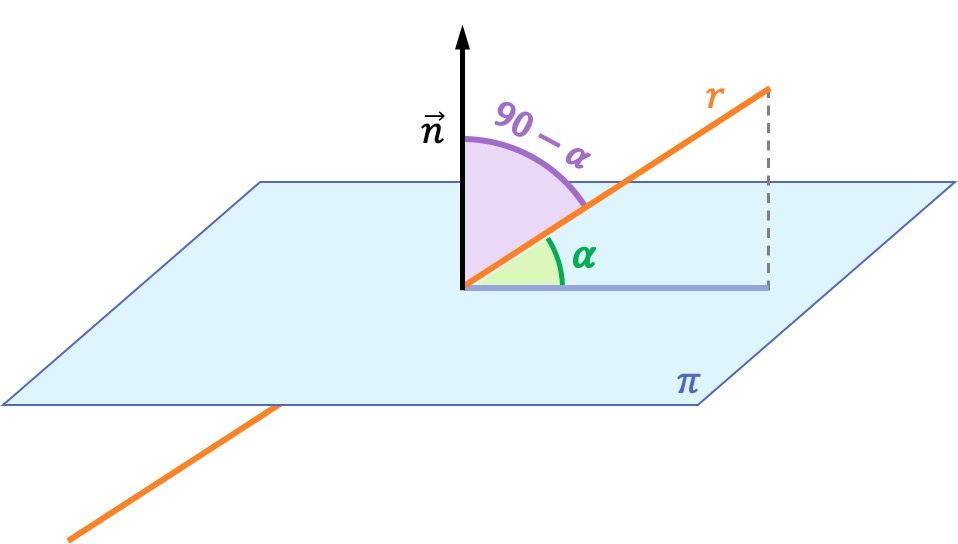
que es el angulo entre una recta y un plano

El ángulo entre una recta y un plano es el complementario del ángulo que forman dicha recta y el vector normal al plano. Por lo tanto, el ángulo entre una recta y un plano se calcula a partir del ángulo que forman el vector director de la recta y el vector normal del plano.

Fórmula del ángulo entre una recta y un plano

Para deducir la fórmula del ángulo entre un plano y una recta es necesario que sepas cómo hallar el ángulo entre dos vectores. En la página enlazada encontrarás la explicación junto con ejemplos y ejercicios resueltos paso a paso, por lo que si no recuerdas cómo se hace te recomendamos que le eches un vistazo.

Así pues, como el ángulo entre una recta y un plano es complementario al ángulo entre el vector director de dicha recta $(\vv{\text{v}}_r)$ y el vector normal a dicho plano $(\vv{n})$ , a partir de la fórmula del ángulo entre dos vectores se deduce que el ángulo entre una recta y un plano es equivalente a la siguiente expresión:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Por lo tanto, la fórmula del ángulo entre una recta y un plano es la siguiente:

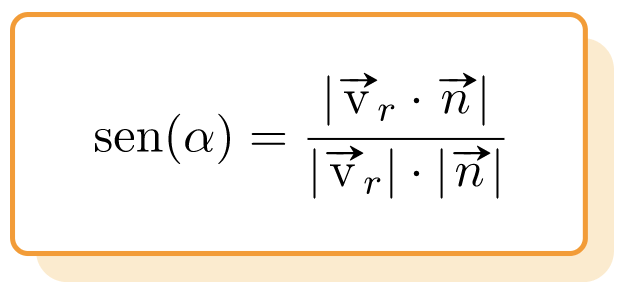
angulo entre una recta y un plano formula

Donde:

$\vv{\text{v}}_r$ es el vector directa de la recta.
$\vv{n}$ es el vector normal al plano.

Ejemplo de cómo calcular el ángulo entre una recta y un plano

Para que puedas ver cómo resolver este tipo de problemas, a continuación tienes un ejemplo del cálculo del ángulo entre una recta y un plano:

Calcula el ángulo que forma la recta $r$ con el plano $\pi.$ Siendo sus ecuaciones:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

La recta está expresada en forma de ecuaciones paramétricas, así que su vector director es:

$\vv{\text{v}}_r = (-1,4,-3)$

Por otro lado, el plano está definido en forma de ecuación implícita (o general), por lo que su vector normal es:

$\vv{n} = (1,-1,4)$

Entonces, una vez conocemos el vector director de la recta y el vector normal del plano, aplicamos la fórmula del ángulo entre una recta y un plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Sustituimos los vectores en la fórmula:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

Y hacemos los cálculos:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Finalmente, invertimos el seno con la calculadora y hallamos el valor del ángulo:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

De manera que el ángulo entre la recta y el plano es aproximadamente 51,80º.

Hay que tener en cuenta que si alguna vez obtenemos un resultado de 0º, significa que la recta y el plano son paralelos o que la recta está contenida en el plano. Y si el ángulo es igual a 90º, implica que la recta y el plano son perpendiculares.

Ejercicios resueltos del ángulo entre una recta y un plano

Ejercicio 1

Halla el ángulo que forma la recta $r$ con el plano $\pi.$ Siendo sus ecuaciones:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

Ver solución

La recta está expresada en forma de ecuación continua, así que su vector director es:

$\vv{\text{v}}_r = (2,-1,-3)$

Por otra parte, el plano está en forma de ecuación implícita (o general), con lo que su vector normal es:

$\vv{n} = (3,1,2)$

Entonces, una vez conocemos el vector director de la recta y el vector normal del plano, utilizamos la fórmula del ángulo entre una recta y un plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Finalmente, invertimos el seno y hallamos el valor del ángulo:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Por lo tanto, el ángulo que forman la recta y el plano es 4,10º.

Ejercicio 2

Determina el ángulo que forma la recta $r$ con el plano $\pi.$ Siendo sus ecuaciones:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

Ver solución

La recta está expresada con sus ecuaciones implícitas (o generales), por lo tanto, tenemos que hallar el vector director de la recta calculando el producto vectorial de los vectores normales a los 2 planos que determinan la recta:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

Por otra parte, el vector normal al plano es:

$\vv{n} = (-4,2,0)$

Entonces, una vez conocemos el vector director de la recta y el vector normal del plano, utilizamos la fórmula del ángulo entre una recta y un plano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Finalmente, invertimos el seno y hallamos el valor del ángulo:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Por lo tanto, el ángulo que forman la recta y el plano es de 46,33º.

Ejercicio 3

Encuentra, mediante la fórmula del ángulo entre una recta y un plano, el valor de $k$ necesario para que la recta $r$ y el plano $\pi$ sean paralelos.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

Ver solución

En primer lugar, la recta está expresada en forma de ecuación vectorial, así que su vector director es:

$\vv{\text{v}}_r = (4,-1,3)$

Por otra parte, el plano está en forma de ecuación general, con lo que su vector normal es:

$\vv{n} = (4,3,k)$

Entonces, para que los dos elementos geométricos sean paralelos, el ángulo entre ellos debe ser cero. Por lo tanto, la fórmula del ángulo entre una recta y un plano queda de la siguiente manera:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

De modo que el producto escalar entre el vector director de la recta y el vector normal debe ser nulo. Y a partir de esta ecuación podemos determinar el valor de la incógnita $k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Por último, si te ha resultado útil este artículo probablemente también estés interesad@ en cómo averiguar el ángulo entre dos planos. En la página del enlace encontrarás una explicación bien detallada junto con la fórmula necesaria para calcular el ángulo entre dos planos diferentes y, además, podrás ver ejemplos y ejercicios resueltos paso a paso para poder practicar y entender cómo se hace a la perfección.

Ángulo entre una recta y un plano

¿Cuál es el ángulo entre una recta y un plano?

Fórmula del ángulo entre una recta y un plano

Ejemplo de cómo calcular el ángulo entre una recta y un plano

Ejercicios resueltos del ángulo entre una recta y un plano

Ejercicio 1

Ejercicio 2

Ejercicio 3

Deja un comentario Cancelar respuesta