Sistema de coordenadas

En esta página explicamos qué es un sistema de coordenadas y, además, encontrarás todo sobre el sistema de coordenadas cartesianas. También verás otros tipos de sistemas de coordenadas (polares, cilíndricas, esféricas,…) y las aplicaciones reales que tiene un sistema de coordenadas.

¿Qué es un sistema de coordenadas?

Aunque es un poco difícil de comprender este concepto al principio, la definición de un sistema de coordenadas es la siguiente:

Un sistema de coordenadas es un sistema que nos permite identificar la posición de un punto. Es decir, es un conjunto de valores que se utilizan para definir dónde está situado cualquier objeto geométrico.

Por ejemplo, se puede describir la posición en la que está volando el siguiente avión mediante un sistema de coordenadas:

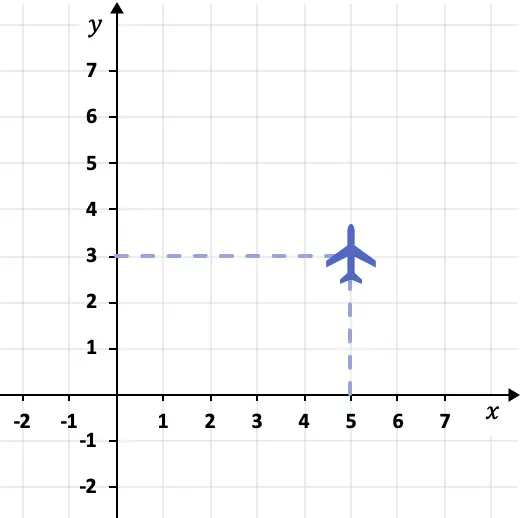
En este caso, el avión se encuentra en el punto (5,3). Porque su coordenada X es 5 y su coordenada Y es 3.

Por otro lado, el punto (0,0) se llama el origen de coordenadas, ya que es donde empiezan los ejes de coordenadas y es el punto de referencia del sistema de coordenadas.

Como curiosidad, se considera que el matemático que inventó el sistema de coordenadas fue el francés René Descartes. Y es por eso que también se denomina sistema de coordenadas cartesiano.

Sistema de coordenadas cartesianas en el plano

La gráfica que hemos visto en el apartado anterior pertenece al sistema de coordenadas cartesianas en el plano. Se dice que es en el plano porque es un sistema bidimensional, o dicho con otras palabras, solo tiene dos ejes: el eje X y el eje Y.

El eje X corresponde a las coordenadas horizontales, mientras que el eje Y representa las coordenadas verticales. A continuación puedes ver varios puntos representados gráficamente con sus coordenadas:

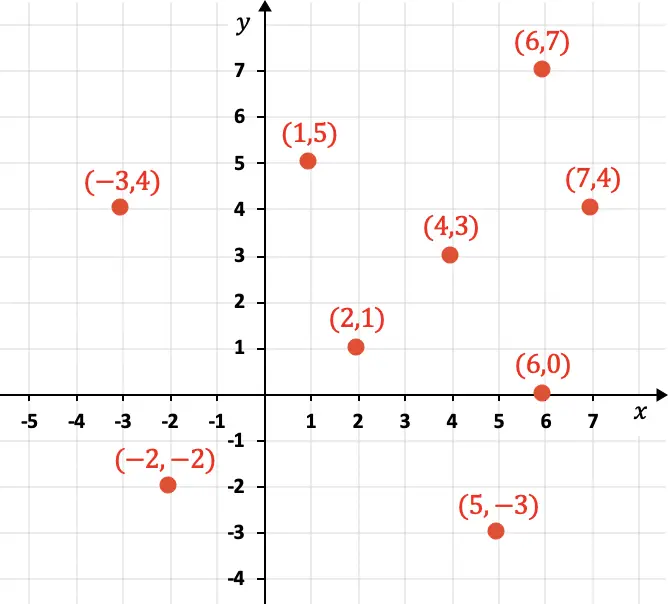
Como puedes ver en el gráfico, las coordenadas se representan numéricamente con un paréntesis, además, primero se pone la componente X y luego la componente Y: (4,3). A parte, las coordenadas pueden ser positivas, negativas o cero.

Por otra parte, este tipo de sistema de coordenadas también se llama plano cartesiano.

Finalmente, debes saber que los ejes de coordenadas se pueden decir de varias maneras, aunque todas significan lo mismo:

• El eje X también se llama eje de las abscisas o eje OX
• El eje Y también recibe el nombre de eje de las ordenadas o eje OY.

Sistema de coordenadas cartesianas en el espacio

Acabamos de ver cómo representar un punto en el plano, es decir, en un sistema de coordenadas con dos ejes (2 dimensiones). Sin embargo, la realidad está formada por 3 dimensiones (altura, ancho y profundidad).

Así pues, en geometría euclidiana el espacio tridimensional se suele representar con un sistema de coordenadas de tres ejes, todos perpendiculares entre sí:

• El eje X representa la profundidad.
• El eje Y indica el ancho.
• El eje Z corresponde a la altura.

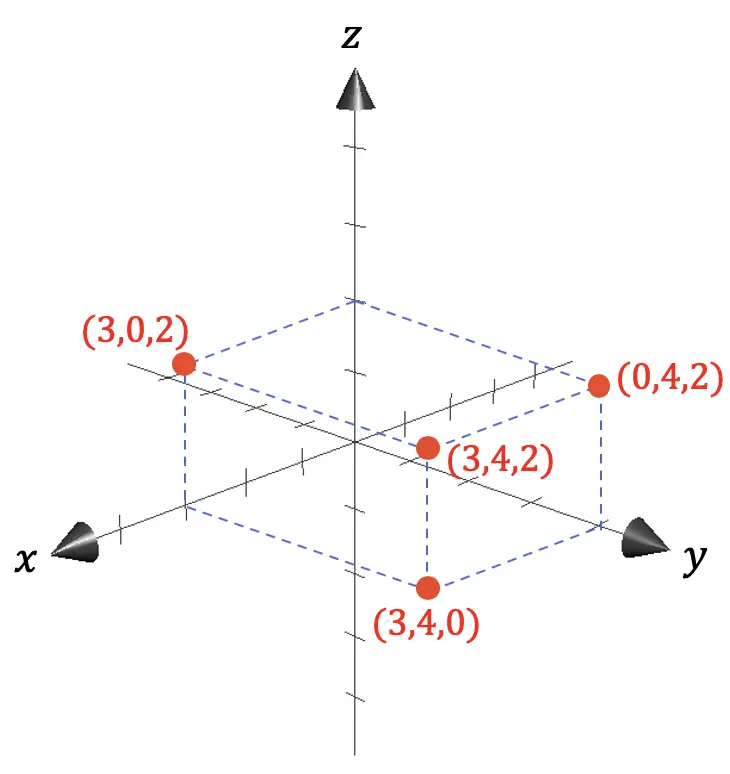
Como puedes apreciar en la representación gráfica anterior, las coordenadas de cualquier punto vienen dadas por las proyecciones sobre los ejes de las distancias entre el punto en cuestión y el origen (0,0,0).

Sistema de coordenadas polares

Los sistemas de coordenadas cartesianos, ya sea en 2D o en 3D, son los más utilizados. Pero en algunas ocasiones nos puede convenir usar otro tipo de sistema de coordenadas.

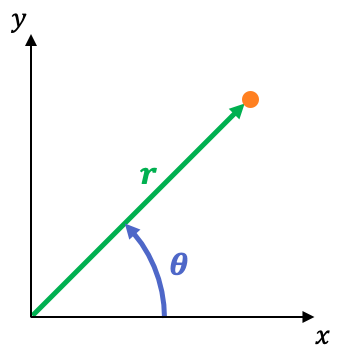
El sistema de coordenadas polares es un sistema de referencia bidimensional cuyas coordenadas son:

• es la distancia entre el origen de coordenadas y el punto. Se denomina coordenada radial.
• es el ángulo que forma el eje X con la recta que pasa por el punto y el origen. Se llama coordenada angular o azimutal.

Se puede pasar fácilmente del sistema de coordenadas rectangulares al de coordenadas polares mediante las siguientes ecuaciones:

Sistema de coordenadas cilíndricas

El sistema de coordenadas cilíndricas es muy parecido al de coordenadas polares. De hecho, es igual pero con una coordenada más: la altura.

De manera que el sistema de coordenadas cilíndricas es un sistema de referencia tridimensional, es decir, con 3 coordenadas:

• es la proyección ortogonal del punto en el plano XY, o dicho de otra forma, la distancia del punto al eje Z.
• es el ángulo que forma el semieje X positivo con la recta
• es la altura del punto, es la misma coordenada del sistema de coordenadas cartesiano en el espacio.

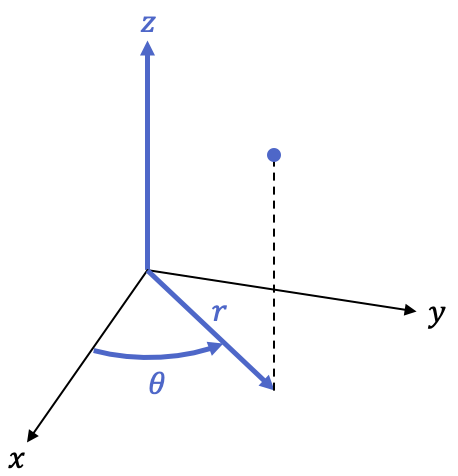
Las siguientes fórmulas sirven para transformar el sistema de coordenadas cartesiano en coordenadas cilíndricas:

Sistema de coordenadas esféricas

Finalmente, tenemos el sistema de coordenadas esféricas. Este tipo de sistema de coordenadas también es bastante similar al de coordenadas polares y al de coordenadas cilíndricas, aunque, evidentemente, tiene alguna diferencia respecto a ellos.

El sistema de coordenadas esféricas se trata de un sistema para describir espacios euclidianos tridimensionales, por lo tanto, tiene tres coordenadas:

• es la distancia (en R3) desde origen hasta el punto.
• es el ángulo que forma la parte positiva del eje X con la recta proyectada en el plano XY.
• es el ángulo que hay entre la parte positiva del eje Z con la recta

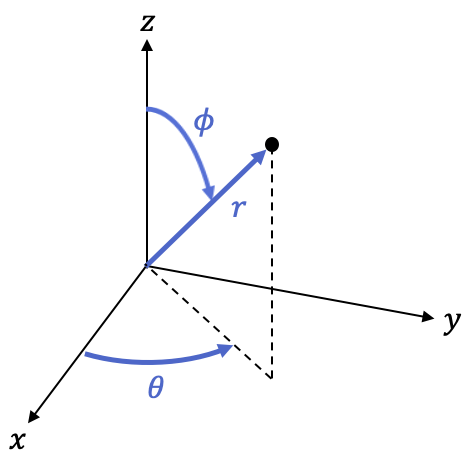
Se puede conmutar entre coordenadas esféricas y cartesianas mediante las siguientes fórmulas:

Aplicaciones reales del sistema de coordenadas

Los sistemas de coordenadas son tan importantes en matemáticas porque también se utilizan en la vida real. Por ejemplo, son útiles para localizar objetos, personas o incluso sitios en un mapa. De hecho, los GPS existen gracias a los sistemas de coordenadas, ya que es lo que usan para saber tu ubicación en la Tierra.

Concretamente, los coordenadas geográficas de los GPS están formadas por dos componentes: la latitud y la longitud. La latitud (norte o sur) y la longitud (este u oeste) son dos coordenadas angulares que miden el ángulo que hay desde el centro de la Tierra hasta tu posición. Ambas se expresan en grados, ya sea en coordenadas decimales o coordenadas sexagesimales.