En esta página se explica cómo multiplicar un vector por un número real (o un escalar) tanto numéricamente como gráficamente. Además, también encontrarás ejemplos y ejercicios resueltos del producto de un vector por un escalar. Finalmente, también se explica cuáles son las propiedades de este tipo de operación con vectores.
Índice
¿Cómo se multiplica un vector por un número real?
Para calcular el producto de un vector por un número (o un escalar) numéricamente se debe multiplicar cada componente del vector por el número.
De manera que el resultado de la multiplicación de un vector por un número da lugar a un nuevo vector con las siguientes características:
- El resultado del producto de un vector por un escalar origina un nuevo vector con igual dirección que el vector original.
- Además, el nuevo vector tendrá el mismo sentido si el número es positivo.
- O tendrá el sentido contrario si el número es negativo.
- El módulo del vector resultante es equivalente al módulo del vector original multiplicado por el escalar.
En la siguiente representación gráfica puedes ver como la dirección del vector se mantiene independientemente del signo del escalar. En cambio, el sentido del vector sí que depende del signo del número que multiplica.
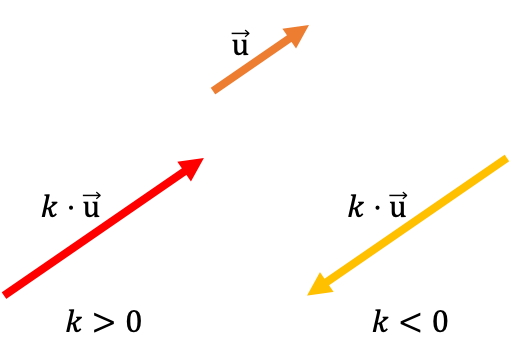
También, en el siguiente gráfico se ve claramente que el módulo del vector resultante del producto es igual al módulo del vector original multiplicado por el escalar.
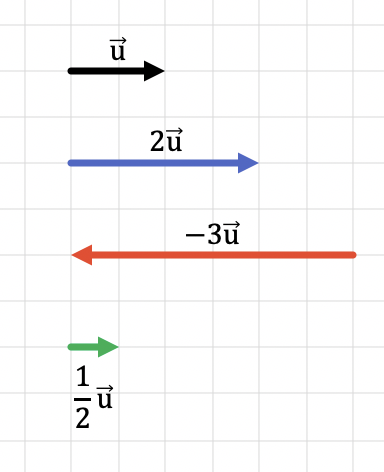
Evidentemente, si multiplicamos el vector por un número más grande que 1, el resultado es un vector de mayor longitud (de mayor módulo). Por contra, si multiplicamos el vector por un número más pequeño que 1, entonces el resultado es un vector de menor longitud (menor módulo).
Nota: no hay que confundir el producto de un vector por un escalar con el producto escalar de vectores. Aunque tienen un nombre parecido, son dos conceptos totalmente diferentes.
Ejemplo del producto de un vector por un escalar
A continuación vamos a ver un ejemplo numérico de cómo se calcula el producto de un vector por un número:
- Multiplica el siguiente vector por 4:
Como has podido comprobar, este tipo de operación vectorial no es muy complicada, porque no se tienen que hacer muchos cálculos.
Sin embargo, existen operaciones de vectores más complicadas, como la suma de vectores y la resta de vectores. Si ya has entendido cómo se calcula el producto de un vector por un escalar, te recomendamos que pases al siguiente nivel y consultes cómo se resuelve la suma vectorial y la resta vectorial, ya que son un tipo de operaciones un poco más difíciles y, de hecho, se utilizan mucho más (son más importantes).
Propiedades de la multiplicación de un vector por un número
El producto de un vector por un número posee las siguientes propiedades:
- Propiedad asociativa: cuando se multiplica el vector por más de un número, es indiferente el orden de las multiplicaciones.
- Propiedad distributiva respecto a la suma y a la resta de vectores:
- Propiedad distributiva respecto a la suma de escalares:
- Elemento neutro: obviamente, cualquier vector multiplicado por 1 da como resultado el propio vector:
Ejercicios resueltos de multiplicación de un vector por un escalar
Ejercicio 1
Calcula analíticamente el resultado del producto del siguiente vector por 3:
Para hallar el producto debemos multiplicar cada coordenada del vector por 3:
Ejercicio 2
Multiplica el siguiente vector por 6 y encuentra su módulo:
Primero hacemos la multiplicación del vector por el escalar:
Ahora existen dos formas de calcular el módulo del vector obtenido. La primera es hallar el módulo del vector original y luego multiplicarlo por 6:
Y la segunda manera es calcular directamente el módulo del vector obtenido en la multiplicación:
De modo que con los dos procedimientos queda demostrado que el resultado no depende del método por el que se calcule el módulo.
Ejercicio 3
A partir del siguiente vector:
Calcula las siguientes operaciones algebraicamente:
Luego, determina si los vectores resultantes tienen la misma dirección y el mismo sentido que el vector original y ordénalos de menor a mayor longitud.
Primero calculamos las multiplicaciones:
Por lo tanto, los vectores multiplicados por números positivos tienen la misma dirección y el mismo sentido que el vector original. Y los vectores multiplicados por números negativos tienen la misma dirección pero el sentido opuesto al vector original.
Vectores con misma dirección y mismo sentido: y
Vectores con misma dirección pero distinto sentido:
Finalmente, hay que ordenar los vectores según su longitud, o equivalentemente, su módulo. El vector con más longitud (o mayor módulo) será el que se ha multiplicado por un número más grande (en valor absoluto), y el vector con menor longitud (o menor módulo) será el que se ha multiplicado por un número más pequeño (en valor absoluto). De forma que el orden de longitudes es:
Fíjate que la longitud o módulo no depende del signo del escalar que multiplicaba, ya que el sentido del vector no modifica su módulo.
Ejercicio 4
Dados los siguientes dos vectores:
Calcula la siguiente operación:
Primero resolvemos las multiplicaciones de vectores por números:
Y luego restamos los vectores:
Ejercicio 5
Realiza las siguientes multiplicaciones de vectores por escalares y representa los resultados gráficamente:
Primero hacemos las multiplicaciones de los vectores por los escalares reales:
Por último, una vez hemos calculado los vectores, los representamos en el gráfico:
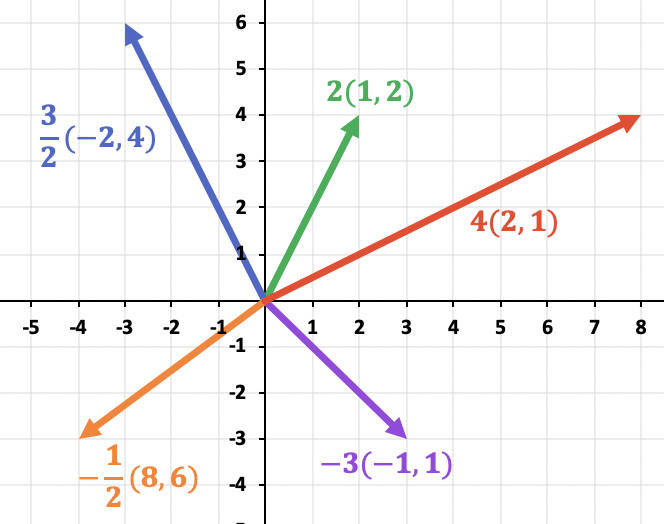


Muy buena y didáctica la explicación… Mi sugerencia será en añadir la representación gráfica de la operación!!!! Mil gracias y felicitaciones…
¡Muchas gracias Maikel!
Al principio de la página también hemos explicado cómo se multiplica un vector por un número de forma gráfica. Pero gracias por tu aportación, ¡se agradece toda contribución a mejorar la página!